Stereophile
Vol.9 No.6, September 1986
Zen & The Art of D/A
Conversion
By John Atkinson
It has become accepted lore in audiophile circles that the 44.1kHz sampling
rate adopted for Compact Disc is too low. Some writers have argued that,
as a 20kHz sinewave will only be sampled about twice per cycle, it will
not be reconstructed accurately, if at all.
Now, it may be true that 44.1kHz is too low a sampling rate, but certainly
not for this reason. H. Nyquist, a researcher at Bell Labs, many
years ago proved mathematically that as long as the sampling frequency
is at least twice the highest frequency of interest in the signal to be
sampled, the waveform will be accurately preserved. This
was verified by JGH in his original review of the Sony PCM-F1 (Vol.5 No.7),
but is hard to grasp emotionally---I mean two samples don't sound anything
like enough! Here, then, is an elegant explanation I heard a little while
ago, courtesy of Stanley Lipshitz of the Audio Engineerng Society
and the University of Waterloo.
I'll start by assuming that we have something that doesn't exist: an audio signal with a spectrum that has no components above half the sampling frequency (fig.1). (Those who complain that picking a signal that doesn't exist to prove the case have a point; I will merely say that true scientific method always involves leaving out messy facts that confuse things unnecessarily. And you're going to get a few more such examples in this piece.)
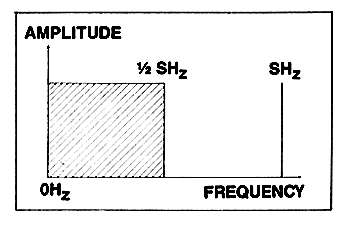
Fig.1 Spectrum of input signal band-limited to half sampling
frequency (s).
Using a perfect A/D converter---I told you there'd be more convenient simplifications---the signal is duly sampled and encoded, producing a mass of data consisting of a regular string of numbers. Each number describes how big the signal is at a time interval 1/s seconds after the last one ("s" is the sampling frequency). In order to reconstruct the signal, this stream of data is fed to a perfect D/A converter which, in its simplest form, spits out an infinitely narrow pulse every 1/s seconds, the height of the pulses roughly mapping out the original shape of the signal (fig.2).
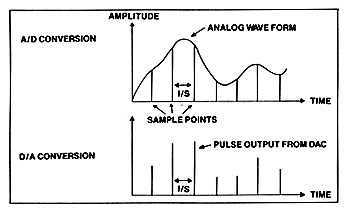
Fig.2
To reconstruct the waveform properly, we again need something that doesn't
exist: a perfect low-pass filter with the impulse response shown
in fig.3.
Note that whereas we could imagine that somebody, somewhere,
will eventually design a perfect A/D converter, this perfect filter's impulse
response has a feature that doesn't exist in nature---ever!
It appears to know that a pulse is about to happen---as with the mythical
chemical substance postulated by Isaac Asimov that dissolved just
before the experimenter added water. (Footnote 1)
The perfect filter starts to oscillate with increasing amplitude before
the pulse occurs. When the pulse finally happens along, the filter's oscillation
reaches a maximum, then dies away in a perfect mirror image of its precognitive
behaviour.
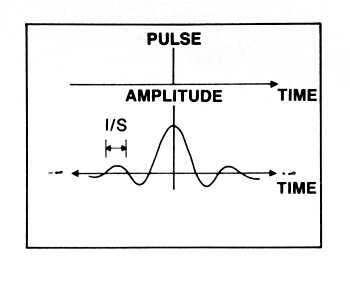
Fig.3 Perfect low-pass filter impulse response.
The actual shape of the response is called a (sin x)/x curve,
and extends in time from minus infinity to plus infinity. As we are dealing
with imaginary circuits, it is no sweat to define that the zeros
in the (sin x)/x response---the points where the amplitude of the oscillations
are zero---are spaced 1/s seconds apart. If we feed our stream of pulses
of varying heights, representing the signal, into this filter, then each
pulse will produce a (sin x)/x wave that will be zero every time another
pulse comes along. It will not be zero in-between the pulses, as shown
by fig.4, and if all these nonzero waves are added together,
the sum of their amplitudes exactly reconstructs the shape of the
original wave between the sampling points. I'll leave it to you to do the
sums for a 20kHz sinewave sampled at 44.1kHz---give your PC a workout---but
the important thing is that there is no missing information about the shape
of the original waveform up to its bandlimit of 22.05kHz. Despite the fact
that a 20kHz sinewave is only sampled twice per cycle.
Elegance indeed---a marriage made in Heaven (or Bell Labs) between
a perfect pulse stream and a perfect low-pass filter!
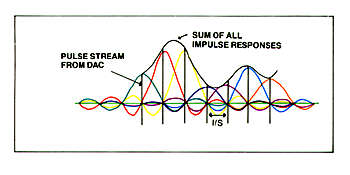
Fig.4 Waveform reconstructed by perfect low-pass filter.
But wait! This elegance exists only on paper.
Our original signal doesn't exist; we used a perfect A/D converter;
we assumed that the string of numbers didn't become corrupted in storage;
our D/A converter produced infinitely narrow pulses, spaced exactly 1/s
seconds apart; and our reconstruction filter featured a perfect impulse
response extending to infinity in both time directions with zeros also
spaced exactly 1/s seconds apart.
On paper, everyone's CD player produces a perfect sound forever.
In reality---well, this issue of Stereophile already contains
enough discussions of the subjective shortcomings of the medium.
Yes, I know---there are tens of thousands of happy CD player owners.
But you should now start to see why there are subjective shortcomings.
Take the first assumption, that the signal had no components above half
the sampling frequency. Real music inconveniently has a spectrum that extends
up and up, well above the traditional "20 to 20k" audio bandwidth. Before
it can be sampled, the music signal has therefore to be viciously filtered
to avoid the particularly audible nasties of "aliasing"---such a
benign word to describe one of the more unpleasant-sounding distortions---and
the design of such filters is no trivial task.
They ring; they produce gross phase shift in the audio band; they go
out of alignment; if they have major ripples in their passband's amplitude
response, these inconveniently show up in the digital domain as pre- and
post-echoes (a phenomenon described by its rediscoverers, Roger Lagadec
and Thomas Stockham, as "dispersion"); and, most important,
the only way around these problems costs money---lots of it.
If only the CD sampling rate were higher than 44.1kHz, the digital
recorder's input anti-aliasing filter problems could at least be moved
farther away from the music, which is the real reason why the sampling
frequency is too low.
I'll draw a discreet veil over the "perfect" A/D converter and data storage required---I live in hope.
The rest of the process you get for free when you buy a CD player. The perfect D/A converter---see my comment on its A/D equivalent. (Of one thing I am sure: you can't buy one for the kind of money available to a manufacturer marketing a CD player for $349, let alone $149.)
How about some of the minor impossibilities? The fact that the pulses coming from the DAC should be infinitely narrow turns out not to present a major problem. Even if the pulse is so broad that it lasts until the next one, producing a "staircase" waveform, the only effect is to droop the treble somewhat, about 4dB at 20kHz, the kind of problem that circuit designers are good at solving. The fact that the pulses should be spaced exactly 1/s seconds apart turns out to be much more serious. As pointed out by Philip Greenspun in the Winter 1986 issue of The Computer Music Journal, and discussed by Bob Stuart in Stereophile (Vol.9 No.2), any minor inconsistency in timing---due, say, to jitter in the player's crystal-controlled clock from heavy current demands on an inadequate power supply---means losing precision in the reconstruction of the fine detail of the analog signal. Engineers call this "distortion."
Now that you've accepted the fact that the
existence of a precognitive reconstruction filter is an impossibility,
look at the measured impulse response of a Philips-system CD player
(fig.5).
Familiar, huh?
It turns out that one of the beauties of a signal once it is in the
digital domain is that the direction of time flow no longer is an invariable
constant.
There is no reason at all why the music data on a CD can't be played
from end to beginning, decreasing entropy and causing the musicians to
grow younger. Some musical works---Barry Manilow's entire output, for example---might
even sound better! Similarly, consider the steady flow of data through
a CD player's circuits. Animal fanciers could consider the numbers as goats
passing through a door; unless the doorkeeper had X-ray vision, he would
not know anything about a particular goat until it passed through the door.
However, there is no reason at all why the doorkeeper couldn't place a
second door before the first and take some action at the main door based
on what he found out at the second: stop all brown goats from going through,
for example. To an outsider not aware of the existence of the upstream
door, it would appear that the doorkeeper possessed prescience of the color
of approaching but unseen goats.
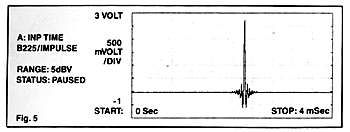
Fig.5
The effect of being able to examine a stream of digital data
anywhere along its length---provided you have enough RAM to hold that data---is
the ability to be able to manipulate time; precognitive
circuitry becomes a possibility.
A filter operating in the digital domain can be made to approximate
perfect behaviour because it can look both back and forward
in
time and operate on the current sample according to what it finds.
In fact, this is the practical basis of digital filtration. The cost
of RAM chips will never fall so low that the filter will be able to operate
from minus infinity to plus infinity, but it can, in practice, ignore
the contributions to the wave shape of samples far away in time from the
current sample, as the resultant error in amplitude will be less
than the random changes due to noise.
The digital filter used by the first generation of Philips players
used 96 coefficients---it could examine 96 samples before and after the
sample of interest simultaneously, in order to act as an ideal low-pass
filter---while the new filter in the true 16-bit players has more,
reaching further toward a better approximation to that perfect impulse
response.
This attempt to approach the theoretical elegance is one reason why
audiophile-quality CD players, or at least CD players with pretensions
to audiophile sound, feature the Philips D/A chip set, which includes the
"precognitive" digital filter. (A perhaps more important
reason is that Philips will actually sell their technology to small hi-fi
companies.) Digital filters are now also appearing in players from Sony
and Technics, some four years after the Dutch engineers at Philips formulated
their system.
Now, are 16 bits sufficient? And what about oversampling? And the quality of the analog circuitry?
--------------------------------------------------------------------------------
Footnote 1:
I can't remember the name of this substance. A free year's supply of
Stereophile to the first reader who can jog my memory. Or send me an aqueous
solution.
Reader's Letters in Vol.9 No.8 (December 1986) in response to the footnote question:
Thiotimoline #1 Editor: In response to JA's request for the name of Isaac Asimov's "mythical chemical substance" ("Zen and the Art of D/A Conversion," Vol.9 No.6), it is thiotimoline, a supposedly ultra-hydrophilic molecule. It was first reported in "The Endochronic Properties of Resublimated Thiotimoline," published in the March 1948 issue of Astounding Science Fiction and reprinted in The Analog Anthology #1 (Davis, 1980). Thank you for this opportunity to combine two of my interests, audio and science fiction. Now how about that free year's subscription to Stereophile?---Will Chamness Ann Arbor, MI
Thiotimoline #2 Editor: I am probably the 789th person to remind you that Dr. Asimov's endochronic substance was thiotimoline. I couldn't locate the article that first reported on it; probably it has crumbled away completely. The enclosed copy of a later article on the micropsychiatric applications of thiotimoline, however, though by now a deep yellow, could be duplicated. May you enjoy it as much as I did 33 years ago.
One reason you probably have received more answers than you really wanted is the high correlation between audiophiles and readers of science fiction. I used to read Asimov and the others while waiting for the soldering iron to heat. Then someone invented circuit boards, transistors, and computerized design, spoiling all the fun. About the same time (causal or reciprocal relationship?), science fiction went off in the opposite direction and became indistinguishable from fantasy.
Anyhow, my thanks to JA for "Zen and the Art of D/A Conversion"---incidentally, is he familiar with Pirsig's Art of Motorcycle Maintenance?---and to all of the other editors and contributors who brighten the pages of Stereophile.---A. Elgin Heinz San Rafael, CA
Thiotimoline #3 Editor: In JA's article on D/A conversion (Vol.9, No.6) he mentioned a substance which dissolved before the addition of water. The name of this substance is thiotimoline and its properties were first accurately described in Isaac Asimov's paper "The Endochronic Properties of Resublimated Thiotimoline," which was published in the March, 1948 issue of Astounding. (Asimov published a total of four papers on thiotimoline, which can be found in the following Asimov compendiums: Only a Trillion, Opus 100, Buy Jupiter and Other Stories.)
Because of the temporal extension of their carbon bonds, thiotimoline crystals dissolve approximately 1.12 seconds before the introduction of a solvent, usually water. The most common use of thiotimoline's endochronic properties is in the construction of "telechronic batteries."
The principle behind the telechronic battery is easy to understand and home experimenters will have no trouble constructing their own. A test tube containing properly purified thiotimoline is placed between a low-powered laser and a photoelectric cell. When the thiotimoline dissolves, 1.12 seconds before the addition of water, the formerly opaque thiotimoline becomes transparent and the photoelectric cell is tripped. This in turn results in water being added to another test tube containing thiotimoline. The thiotimoline in the second test tube will, of course, dissolve 2.24 seconds before water was added to the first tube. By cascading these "endochronometers" it is possible to create a telechronic battery of any desired time constant. Cascading 3215 endochronometers, for example, results in a battery in which the last tube's thiotimoline dissolves about 1 hour before water is added to the first tube.
The enjoyment of music is, of course, the end to which all audiophiles aspire. Unfortunately, most of our time is spent comparing components in order to decide which ones would give us the most enjoyment if only we had the time to listen to them in a relaxed manner. Proper use of the telechronic battery would enable us to make valid decisions without ever having to do any auditioning of the components in question.
Suppose, for example, that you wanted to decide whether to buy a dobler-smith President 5 or a David Goldblume DG20. Proper evaluation of the two components would not take more than 16 hours, including breaks. So you prepare two telechronic batteries with 16-hour time constants. Just before beginning the comparison you vow to add water to battery A if you prefer the President 5 and to battery B if you prefer the DG20. At this point the last photocell in one of the batteries will trip and you will know the results of your comparison test without ever having had to perform it. If neither photocell trips you will know that 16 hours wasn't enough time and you'd have to try again the next day.
By a modified use of this technique it would be possible for audio reviewers to evaluate equipment without wasting their time listening to the components, giving them far more time to investigate methods for taking ten paragraphs to communicate one sentence's worth of ideas.
Experimenters should be warned that thiotimoline can be dangerous. Last week, in the presence of a telechronic battery with a 10-hour time constant, I instructed an assistant to add water to the battery 10 hours hence. Because of the assistant's long history of accuracy, the last photocell tripped immediately. In an effort to show that the telechronic battery could be fooled I then locked the battery in the basement and melted down the only available key. Well, as you probably know, the Chicago area last week suffered the worst flooding in its history...---Scott Soloway Skokie, IL
Stereophile logo and all contents of this site are copyright by EMAPUSA
Inc.