FA: 
Határozzuk meg k számú, azonos amplitúdójú (és zérus fázisú), egymástól  egyenletesen  w frekvencia - távolságra lévõ szinuszos jel összegét.

MO:
Legyen pl. k páratlan, jelölje w0 a sáv közepén(!) lévõ komponens frekvenciáját és vegyünk cos( ) komponenseket.
A szimmetrikusan elhelyezkedõ tagokat

alapján összevonva, a jel

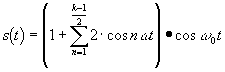
és "mértani sor összege" és az "Euler reláció" felhasználásával  , ahol

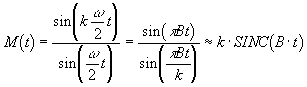,  ha k >> 1, és B = k× (w /2 ×p ) a "sávszélesség".

A multiszinuszos jel M(t) "burkolója" periódikus, mégpedig (k/B) periódusidõvel. A periódusidõ távolságú maximumokat kivéve, zérus-helyeket találunk 1/B távolságokon.

Speciálisan: alapsávi jel, azaz w0/2p = B/2 esetén (és k >> 1 feltétellel)

.

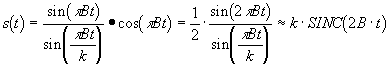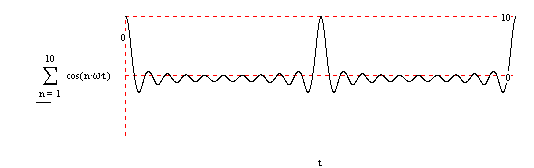
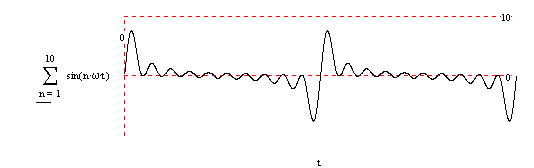
Az alábbi ábra a k = 10 alapsávi esetet szemlélteti:
Megjegyzés: sin( ) komponensek összege esetén az alapsávi jel (k = 10):
Összevetve az elõzõ ábrával, jól megfigyelhetõ: a komponensek fázisának megváltozása - amint ez várható - alapvetõen befolyásolja a jelalak ot !!

e-mail: papay@hit.bme.hu