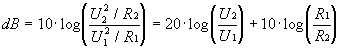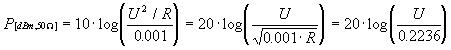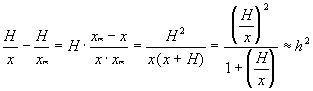"Decibel
(dB)": arány logaritmikus skálán
Everything is relative.
Mottó:
"Baj van a füleddel
, ha nem érted mi a decibel."
 A relatív (hang)teljesítmény mérésére
és összehasonlítására "keletkezett"
eredetileg ez a skála, A. G. Bell-rõl elnevezve.
A relatív (hang)teljesítmény mérésére
és összehasonlítására "keletkezett"
eredetileg ez a skála, A. G. Bell-rõl elnevezve.
( Invented by engineers of the Bell Telephone Laboratory, it
was originally called the transmission unit
or TU, but was renamed in 1923 or 1924 in honour of the laboratory's
founder and telecommunications pioneer Alexander Graham Bell.
Martin, W.H. : "DeciBel - the new name for the transmission unit".
Bell System Tech. J. , January, 1929.
Prior to 1923, tel[efon]co[mpanie]s used a "standard cable
mile" (SCM) characteristic to figure signal losses in telephone wiring.
In 1923, W. H. Martin of Bell Labs defined the Transmission Unit (TU) to
replace the SCM as well as Harvey Fletcher's SU which he defined as a minimum
perceptable change in sound level. By 1929, Martin called the TU the decibel,
as one tenth of a unit named for Bell. )
Köztudottan a fül "igen érzékeny", nagy
dinamikát visel el és közel logaritmikus átvitelû.
A méréstechnikában ennél szélesebb
körû a decibel használata. Itt röviden az alapismereteket
foglaljuk össze.
Definíciók,
oda-vissza
Két teljesítmény-szint
aránya dB-ben:
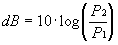 és
és 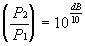
Gyakran praktikusabb P
= U2/R (ahol U: effektív
érték) felhasználása:
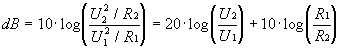
Érdemes megjegyezni: 10dB
éppen 10:1 teljesítmény
aránynak felel meg, és ez az egyetlen pont, ahol megegyezik
a "dB " és az "arány" számértéke.
Ha a teljesítmény felére
csökken, az -3 dB változást jelent.
Decibel
és felbontás
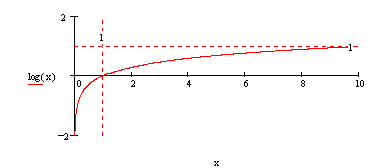
A felbontás (ami durván:
két egymáshoz közeli érték megkülönböztethetõségét
jelenti), fontos méréstechnikai jellemzõ. Értékét
1-nek véve és a tartományban mérhetõ
maximális értékhez viszonyítva, jól
jellemzi a mérési eljárás relatív
érzékenységét.
Például, 4000 digit
(számjegy) tartományú DVM (Digitális VoltMérõ)
névleges felbontása 4000:1, vagyis 72 dB
. Ennek reciprokaként is specifikálják ezt az
adatot, ugyanazt tehát másképp: a felbontás
1 a 4000-bõl , azaz -72 dB.
Másik példa:
n bites analóg-digitális(A/D) átalakító
2n különbözõ mérõszámot
generálhat, 20×
log(2n/1) = 6×
n, azaz "bitenként 6 dB
" a dinamika javulás.
Megjegyzés: a felbontást
gyakran %-ban (% = 10-2), az "igen
jó" felbontást pedig ppm-ben is mérik
(ppm : parts per million =
10-6 ).
Hiba és
decibel
Kétféle módon
is szokás a hibát dB-ben megadni; szerencsére
maga az érték-nagyság tájékoztat
az értelmezésrõl.
A hagyományos additív
hiba modell szerint
"mért érték
= mérendõ(x) ±
hiba(H)"
(1
) A hibás érték [azaz a mért érték
(x ±
H)] aránya a helyes (x) értékhez:
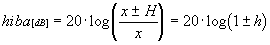
ahol h: relatív
hiba (= h[%]/100 ) és h < 1 (sõt, rendszerint
h <<
1).
Ez az arány tehát
1-hez közeli értékû, ezért ilyenkor
0dB -hez közeli az eredmény,
és "amennyire 0dB, annyira
hibátlan". Az elõjel követi a hiba elõjelét,
a log függvény nemlinearitása miatt viszont
az eltérõ elõjelû értékek nagysága
különbözik (jól érzékelhetõen
nagy h esetén).
(2
) Magát a hiba abszolút értékét
(| H|) hasonlítjuk a helyes (x) értékhez:
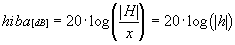
Mivel |h|
<< 1, ezért
ebben az esetben negatív
és nagy értékû
a dB-ben megadott adat. (Megjegyzés: a log
függvény argumentuma csak pozitív lehet.)
Például 1%
-os hiba közelítõleg 0.1 dB [pontosan:
20 ×
log(1 ±
0.01) = +0.0864 ill. -0.0873], vagy ha ez
torzítási adat, akkor -40 dB szintû
a zavaró komponenes [20 ×
log(0.01) = -40 ].
"Abszolút"
decibel értékek, referencia szintek
A decibel, definíciója
szerint, két érték arányát reprezentálja,
tehát relatív "egység". Ha rögzítjük
a referencia nagyságát, akkor alkalmas "abszolút"
teljesítmény vagy feszültség érték
megadására is:
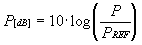 illetve
illetve 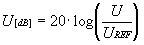
Általában a megnevezésrõl
(az elõre megkötött értékre utaló
jelbõl) ismerhetõ fel az alkalmazott referencia.
(1
) dBm (teljesítmény "egység"):
Gyakori teljesítmény
referencia: PREF =
1mW
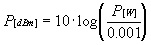 és
és 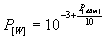
A teljesítményt
disszipáló ellenállás érdektelen.
Ennek konkrét értéke akkor szükséges,
ha a teljesítmény megadását feszültség
mérésre vezetjük vissza, azaz P[W]
= U2/R és U =
effektív érték; ha például
R = 50W
, akkor
(2
) dBV (feszültség "egység"):
A leggyakoribb feszültség
referencia: UREF =
1V effektív érték
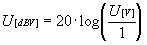 és
és 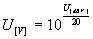
Érdektelen az impedancia.
Persze, konstans dBV különbözõ impedanciákon
eltérõ teljesítményt "szállít".
-120 dBV értékû
az 1 m
V feszültségû
jel. (Ha UREF=1
m V
, akkor az "egység" dB
m V
.)
(3
) dBm/dBV konverzió:
Specifikálni kell az impedanciát! Láthatóan,
a [dBm, RW
] és a [dBV]
kifejezés csak konstans értékkel különbözik,
vagyis:
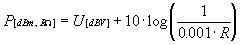
Speciálisan: P [dBm,50
W ]
= U[dBV] + 13.01,
P [dBm,75
W ]
= U [dBV] + 11.25,
P[dBm,600W
] = U
[dBV] + 2.22, P
[dBm,1200 W
] = U
[dBV]- 0.79
Például:
adjuk meg dBVés dBm egységben
a következõ mért értékeket:
(a
) 3.5 Veff feszültség ismeretlen
impedancián,
(b
) 0.2 Veff feszültség
150 W
-on,
(c
) 9 mW teljesítmény 75
W-on.
Válasz:
(a
) U[dBV] = 20×
log(3.5/1) = 10.9, P
[dBm] nem határozható meg(!)
(b
) U[dBV] = -14, P[dBm,150
W ]
= 20×
log(0.2/0.3873) = -5.7
(c
) P[dBm] = 10×
log(0.009/0.001) = 9.5,
U [dBV] = P[dBm,75
W ]
- 11.25 = -1.75
(4
) néhány további, gyakran használt "egység":
dBFS :
FS : Full Scale
(végérték) a referencia
dBu ("dee-bee-you"):
u: unit or unterminated
, feszültség referencia: U
REF = 0.775 V
Ez 600
W -on 1mW (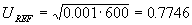 V), vagyis 600 W
-on dBu és dBm numerikusan ekvivalens,
de a dBu feszültség "egység"
semmit sem tételez fel az impedanciáról!
dBc :
c : carrier (vivõ)
szintje a referencia
V), vagyis 600 W
-on dBu és dBm numerikusan ekvivalens,
de a dBu feszültség "egység"
semmit sem tételez fel az impedanciáról!
dBc :
c : carrier (vivõ)
szintje a referencia
dBr :
r (= re): relative
, azaz az alkalmazáshoz külön adják
meg a referencia értékét ( vagy az a "0 dB
" alapján ismerhetõ fel!)
Néhány
feladat
- Adjuk meg dB-ben
a ±
20 % hiba specifikációt!
- Igazoljuk: R
[ W
] ellenálláson
P[dBm] teljesítmény
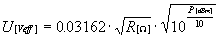
 A relatív (hang)teljesítmény mérésére
és összehasonlítására "keletkezett"
eredetileg ez a skála, A. G. Bell-rõl elnevezve.
A relatív (hang)teljesítmény mérésére
és összehasonlítására "keletkezett"
eredetileg ez a skála, A. G. Bell-rõl elnevezve.