MÉRÉSTECHNIKA tárgy
Villamosmérnöki szak, nappali II. évf. 4. szem . (tavaszi félév)
Fakultatív gyakorlat (2. rész)
A
file-ok olvasásához Adobe® Acrobat Reader szükséges.
Témakörök:
1. Idõ(tartam), frekvencia (gyakoriság) mérés
2. Digitalizálás (I)
3. Digitalizálás (II)
4. Oszcilloszkóp (I)
5. Oszcilloszkóp (II)
6. Spektrumanalizátor, Jelgenerátor
99/04/12
1: Idõ(tartam), frekvencia (gyakoriság) mérés
F1.1: Határozzuk meg a kapuzott esemény-számlálás (a "szorzat-szabály") mûveletnél fellépõ (numerikus)hiba eloszlását. (Elõször az ún. csatorna profilt: a mérõszám feltételes (bemenettõl függõ) valószínûségét számítsuk ki.)
Ennek alapján értékeljük a méréstechnikai gyakorlatban szokásos "a hiba +/-1 " specifikációt. Feltétel: a start-bizonytalanság egyenletes eloszlású.
Megjegyzés: az eredmény ún. Simpson (háromszög) eloszlás.[Tudunk erre más gyakorlati példát is találni? > probability distribution of two dice ]
Fontos: a hiba tehát nem Gauss (normál) eloszlású.Az ideális kvantálás (kerekítés) hibája egyenletes (négyszög) eloszlással becsülhetõ, ettõl miért tér el az itt vizsgált eset?
Legyen a frekvencia a mérendõ paraméter és értéke konstans: f = 12.34 kHz, a kapuidõ pedig to = 0.01 s. Milyen mérõszám(ok) mekkora valószínûséggel lép(nek) fel?
Fogas kérdés: hogyan módosul a hiba-eloszlás, ha nem ideális, hanem véges szélességû eseményeket (valóságos impulzusokat) számlálunk és emiatt a kapuzásnál pulzus-csonkítás, és ebbõl adódóan esemény-vesztés is felléphet? (Javasoljunk módszert ennek megszüntetésére.)
F1.2: "Univerzális számláló" integrált áramkör:
ICM7226 10 MHz Universal Counter System
F1.3: Frekvenciamérõ:
Model 232FC RS-232 Port-Powered Frequency Counter
F1.4: Feszültség - frekvencia átalakító (VFC ) alkalmazása.
Unipoláris (ún. töltés-visszacsatolás elvû) VFC, bipoláris bemenõ jel kezelése és automatikus nulla-pont korrekció (AutoPolarity, AutoZero).Megjegyzés: "feszültség - gyakoriság (frekvencia) - átlagolás (szûrés)" mûveletsor adja a mérõszámot, amelynek felbontása az átlagolás (a kapuidõ) függvénye. (Találjunk gyakorlati példát a célszerû kapuidõ választásra.)
Ha például zavarérzéketlen átvitel, illetve galvanikus elválasztás kell az érzékelõ és az adatfeldolgozó között, akkor miért célszerû a VFC módszer?
Hasonlítsuk össze a VFC módszert a feszültség - idõ átalakítású (VTC) ún. dual-slope eljárással.
F1.5: Digitális gyorsulásmérõ:
Model 1010 Digital accelerometer
F1.6: A fázisszög két azonos frekvenciájú jel null-átmenetének idõkülönbségével arányos. Három mérés: PER, TIME A-B, TIME B-A eredményébõl hogyan adható meg (fok-ban) a fázisszög értéke? (Miért célszerû a harmadik mérés?)
F2.1: A jel mintasorozata:, i = 0,1,2 ... Ezt az idõrekordot fc = 8 kHz gyakorisággal rekonstruáljuk. Mennyi a rekonstruált jel pillanatnyi frekvenciája a t = 0.5 s idõpontban? Melyik idõpillanatban lesz a jel pillanatnyi frekvenciája f = 4 KHz?
Megjegyzés: a példa megoldása elõtt három egyszerûbb feladatot oldjunk meg!
(1) A, i = 0,1,2 ... idõrekordot fc = 10 kHz gyakorisággal rekonstruáljuk. Milyen frekvenciájú jelet kapunk? Hány mintát kell tárolni - ebben az esetben - a memóriában?
(2) fs = 8 kHz gyakorisággal mintavételezünk egy három komponensbõl álló jelet, a komponensek frekvenciája f1 = 3 kHz, f2 = 6 kHz, f3 = 7 kHz. Milyen frekvenciákat találunk a mintavételezett jel alapsávi spektrumában?
(3) Adjuk meg egy lineárisan változó frekvenciájú szinuszos jel argumentumát (a fázisfüggvényt). Milyen ennek az értéke nulla start frekvencia és nulla kezdõ fázis esetén?
Útm.: Ez a lineáris frekvencia sweep az ún. chirp-jel. (Az elnevezés az akusztikus tartományban kifejtett hangzásra utal.) Ha a start frekvencia f1, és T (sweep)idõ múlva f2 lesz a frekvencia értéke, akkor a frekvencia-változás meredeksége (sweep rate): S = (f2 - f1)/T. Ezzel könnyen definálható a pillanatnyi frekvencia idõfüggvénye (amely a fázis deriváltjával arányos), ebbõl integrálással kapjuk a fázist. A chirp-jel fázisa kvadratikus függvény.
Lásd ezután a kiinduló feladatot!F2.2: Kétfrekvenciás (azaz két szinusz összegébõl álló) jel komponenseinek amplitúdója, frekvenciája és fázisa rendre: A1 = 1, f1 = 400, f1 = 0, és A2 = 1, f2 = 600, f2 = 0. A jelet fs = 1000 (Hz) gyakorisággal mintavételezzük.
Milyen frekvencia komponenseket találunk a mintavételezett jel alapsávi spektrumában?
Megjegyzés: a feladathoz tartozó Mathcad dokumentum : vudu.zip.F2.3: Szinuszos jelet generáló numerikusan kontrollált oszcillátor (NCO) minta-frissítési gyakorisága: fc, a közvetlenül rekonstruált jel frekvenciája: f > fc/2. Hogyan lehetséges ez?
******************
99/04/26
3 : Digitalizálás (II)
F3.1: 20 kHz-es információs sávszélesség és 16 (effektív)bit felbontás szükséges. Túlmintavételezést követõ digitális szûrés és mintaritkítás (decimálás) módszerrel, mekkora minta-gyakoriságú 12bites (ill. 8 bites) A/D átalakítót kell használni?
Feltétel: folyamatos a mintasorozat, és az A/D hiba spektruma "fehér"-zaj.
Értékeljük gyakorlati szempontból is ezt a megodást!F3.2: Az elõzõ példa szerinti jeldigitalizáláshoz DS (delta-szigma) A/D átalakítót használjunk. A DS módszer a túlmintavételezés mellett zajformálást is végez decimálás elõtt, ilymódon - az információs sávban lecsökkent kvantálási zaj miatt - kisebb A/D bitszám is elegendõ. Legyen 1 bites az A/D és elsõrendû (egyetlen integrálót tartalmazó) DS. Mekkora minta-gyakoriságú A/D átalakító szükséges?
Feltétel: az A/D hiba spektruma "fehér"-zaj. (Ez erõsen kritizálható, de globálisan elfogadható a becslés; lásd még F3.5)Megjegyzés: a megoldás után idézzük fel az F1.4 feladatban megismert tényeket (és lásd F1.5-öt is)!
F3.3: 24 bites, jelkondícionáló digitalizáló:
AD7710 Signal conditioning ADC
F3.4: Flexibilis felbontású digitalizáló:
NI5911 | FlexADC 100 MS/s, 100 MHz 8 to 21-Bit Digitizer
F3.5: A kvantáló (igen erõs nemlinearitás) kis-jelû viselkedését hatásosan javítja a jelhez kvantálás elõtt hozzáadott zaj (dither), amely zajjá konvertálja a (harmónikus) torzítást, és így érvényesül igazán az átlagolás. Tanulmányozzuk a dither hatását a dither.zip Mathcad dokumentum segítségével.
F3.6: A kvantált szinuszos jel torzítási spektruma erõsen bitszám, mintaszám, amplitúdó, fázis és numerikus frekvencia (f/fs arány) függõ. [Lásd pl. a jegyzet DDS Jelgenerátor fejezet Függelék-ében.]
Speciálisan f/fs = 1/4 és zérus fázis esetén NINCS torzítás! Miért?
******************
99/05/03
4 : Oszcilloszkóp (I)
F4.1: Egyszerû kompenzált osztó modellel, határozzuk meg a jelcsatoló 10:1 osztású "mérõfej"(mérõkábel) frekvencia átvitelét. Legyen az oszcilloszkóp bemeneti impedanciája Ri = 1 MW, Ci = 15 pF, a forrás pedig R = 50 W- os (vagy ahogy tesztelésnél szokásos, lezárt 50 W-os, azaz R = 25 W ).
Összehasolításként, adjuk meg a közvetlen (azaz a "mérõkábel" nélküli) jelcsatolás sávszélességét is. (Ne lepõdjünk meg, az ellenállás viszonyok miatt az oszcilloszkóp elsõsorban kapacitív terhelés!)
******************
99/05/10
5 : Oszcilloszkóp (II)
F5.1: "Jegyzet, Oszcilloszkóp fejezet, 35. old.: Test Your Knowledge of DSO."
Az elsõ DSO dátuma: 1972(3), ez a kvíz pedig a 80-as években jelent meg az akkor vezetõ elektronikai hetilapban (Electronics , a lap már megszünt), egy korszerû (ma már nem gyártott) DSO-t tûzve ki nyereményként.
Meglepõen kevesen adtak jó válaszokat, pl. a 8. kérdésre a helyes válaszok aránya csak 19% ...
******************
99/05/17
6 : Spektrumanalizátor, Jelgenerátor
F6.1: "Jegyzet, Spektrumanalizátor fejezet, 14. old.: 6/b példa."
Tanulmányozzuk a NÉGYSZÖG és HANNing idõablak alapvonásait a window.zip Mathcad dokumentum segítségével.F6.2: Hálózati frekvenciás (f = 50 Hz-es) jel m = 7 periódusából N = 29 mintát veszünk. Ebbõl DFT-vel számítjuk az egyoldalas, alapsávi spektrumot (periodogram).
Melyik DFT-bin, azaz hányadik frekvencia index (k = ? egész szám) adja a jelben lévõ negyedik harmónikus komponens (200 Hz) értékét?
Miért célszerû koherens mintavétel (vagyis "egész számú jelperiódusból egész számú minta")?F6.3: Vonalas spektrum k-adik komponense (kompakt alak):
ahol f0 = 1/T 0 az alapharmónikus frekvencia, A k az amplitúdó , f k a fázis, amely ekvivalens egy frekvencia (periódusidõ) függõ tk késleltetéssel: 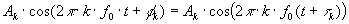
és legyen minden komponensre fk = 0 . Lásd: phase.zip Mathcad dokumentum . 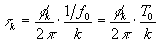
Megváltozik-e a jelalak, ha módosítjuk a fázis értékeket?
Milyen változást várunk, ha pl. minden komponensre azonos: f k = p értéket állítunk? És ha fk = p/2 ?
Megjegyzés: a (relatív) fázis tartománya 0 < fk < 2p (mert a cos függvény 2p szerint periódikus). Viszont a késleltetési idõ lehet olyan, hogy értékébõl a fenti összefüggéssel visszaszámolva a - frekvencia függõ - fázist: fk > 2p is adódhat (amibõl mod 2p szerinti adat a cos függvény argumentuma).F6.4: "Programozható frekvenciájú szinusz generátor" integrált áramkör:
ML2037 500kHz, Serial Input, Programmable Sine Wave Generator with Digital Gain Control
További feladatok:
Jegyzet - "Pápay: Jelalak mérés és szintézis , Mûegyetemi kiadó, 1996 (55026)"
Elektronikus példatár